Bạn đã bao giờ tự hỏi tại sao một doanh nghiệp lại chọn chiến lược giá này thay vì chiến lược khác? Hay tại sao một quốc gia lại quyết định hợp tác hoặc xung đột với quốc gia khác? Lời giải đáp cho những câu hỏi này được tìm thấy trong “Lý thuyết trò chơi” – một công cụ phân tích giúp chúng ta hiểu được hành vi chiến lược trong mọi lĩnh vực, từ kinh tế, chính trị đến kinh doanh, đời sống. Hãy cùng khám phá chi tiết về lý thuyết trò chơi qua bài viết dưới đây bạn nhé!
Lý thuyết trò chơi là gì?
Lý thuyết trò chơi (Game Theory) là công cụ giúp chúng ta hiểu kết quả có thể xảy ra khi đưa ra những quyết định trong các tình huống có nhiều người tham gia. Giống như trong trò chơi, mỗi người (được gọi là “người chơi”) sẽ có những lựa chọn và mục tiêu riêng. Và quyết định của người này sẽ ảnh hưởng đến người khác.
Lý thuyết trò chơi không giúp bạn chiến thắng ai khác, cũng không chỉ ra lựa chọn tốt nhất. Thay vào đó, phương pháp này giúp bạn phân tích các lựa chọn mình có và dự đoán kết quả có thể xảy ra từ mỗi lựa chọn.
Theo trang Indeed, lý thuyết trò chơi trong bài: “What Is Game Theory? (Importance and Applications)” được hiểu như sau:
“Lý thuyết trò chơi là một bộ khung toán học được sử dụng để phân tích hậu quả của các kịch bản ra quyết định nhất định. Thuật ngữ “trò chơi” trong lý thuyết trò chơi bắt nguồn từ các trò chơi cạnh tranh, nơi hai người chơi cố gắng vượt qua nhau thông qua các chiến lược và dự đoán chuyên môn. Lý thuyết trò chơi không được sử dụng để đánh bại đối thủ hoặc thậm chí xác định lựa chọn tốt nhất cho người ra quyết định trong bất kỳ tình huống nào. Thay vào đó, đó là một cách để xem xét những lựa chọn thay thế nào có sẵn cho bạn và kết quả nào có thể phát sinh từ mỗi lựa chọn.”
Lịch sử hình thành lý thuyết trò chơi
Lý thuyết trò chơi là lĩnh vực toán học tương đối mới. Tuy nhiên, phương pháp này có nguồn gốc từ những trò chơi cổ xưa như cờ vua và cờ vây. Các trò chơi này đã được con người chơi trong nhiều thế kỷ, thu hút sự chú ý của các nhà toán học và triết học trong việc phân tích chiến lược, hành vi.
Giai đoạn ban sơ:
- 1713: James Waldegrave đưa ra lời giải minimax đầu tiên cho trò chơi Le Her. Đây là một bước tiến quan trọng trong việc phát triển lý thuyết trò chơi vì nó cho thấy cách có thể phân tích các trò chơi có tổng bằng không (tức là lợi ích của một người chơi bằng với tổn thất của người chơi khác).
- 1920s: Émile Borel định nghĩa khái niệm chiến lược hỗn hợp và bổ sung định lí Zermelo. Đây là những đóng góp quan trọng cho lý thuyết trò chơi vì nó cho phép các nhà toán học phân tích các trò chơi phức tạp hơn với nhiều chiến lược tiềm năng cho mỗi người chơi.
Sự ra đời của lý thuyết trò chơi hiện đại:
- 1944: John von Neumann và Oskar Morgenstern xuất bản tác phẩm “Lý thuyết trò chơi và hành vi kinh tế“. Quyển sách này được xem là nền tảng của lý thuyết trò chơi hiện đại. Nội dung của quyển sách giới thiệu các khái niệm cơ bản như ma trận lợi ích, chiến lược thuần túy và hỗn hợp và cân bằng Nash.
- 1950s: John Nash phát triển khái niệm cân bằng Nash – một công cụ quan trọng để phân tích các trò chơi phi hợp tác. Cân bằng Nash là một tập hợp các chiến lược, trong đó mỗi người chơi không thể cải thiện lợi nhuận của mình bằng cách thay đổi chiến lược của mình trong khi những người chơi khác giữ nguyên chiến lược của họ.
Sự phát triển và ứng dụng:
- 1960s: Reinhard Selten giới thiệu khái niệm lời giải của các cân bằng lý tưởng của các trò chơi con. John Harsanyi phát triển các khái niệm thông tin hoàn toàn và trò chơi Bayesian.
- 1970s-nay: Lý thuyết trò chơi được ứng dụng rộng rãi trong nhiều lĩnh vực như kinh tế, khoa học chính trị, quản trị kinh doanh, sinh học, khoa học máy tính,…
Ví dụ về lý thuyết trò chơi
Mô tả:
Hai tên tù nhân, A và B, bị bắt vì tội cướp ngân hàng. Cảnh sát không có đủ bằng chứng để kết tội cả hai, nên họ quyết định thẩm vấn riêng từng người.
Lựa chọn:
Mỗi tên tù nhân có hai lựa chọn:
- Giữ im lặng (H): không khai báo gì về đồng bọn.
- Phản bội (P): khai báo đồng bọn để nhận mức án nhẹ hơn.
Hệ quả:
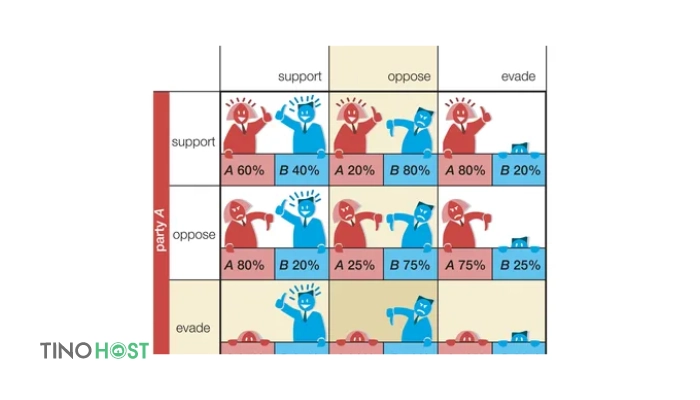
Hệ quả của mỗi lựa chọn được thể hiện trong bảng sau: A/B H P H A: 2 năm tù, B: 2 năm tù A: 8 năm tù, B: Tự do P A: Tự do, B: 8 năm tù A: 4 năm tù, B: 4 năm tù
Phân tích:
- Lợi ích cá nhân: Mỗi tên tù nhân chỉ quan tâm đến lợi ích của bản thân, không quan tâm đến đồng bọn.
- Thiếu thông tin: Mỗi tên tù nhân không biết lựa chọn của người kia.
- Cân bằng Nash: Cả hai tên tù nhân đều chọn lựa chọn tối ưu cho bản thân, dẫn đến kết quả không tốt nhất cho cả hai.
Giải thích:
- Nếu cả hai giữ im lặng (HH): Cả hai sẽ chỉ bị kết tội nhẹ (ví dụ như tàng trữ vũ khí) và chịu án 2 năm tù.
- Nếu A phản bội, B giữ im lặng (PH): A sẽ được tự do, còn B sẽ chịu mức án cao nhất (8 năm tù) vì bị kết tội cướp ngân hàng với đầy đủ bằng chứng.
- Nếu A giữ im lặng, B phản bội (HP): Tương tự như trường hợp PH, B sẽ được tự do, còn A sẽ chịu mức án cao nhất.
- Nếu cả hai phản bội (PP): Cả hai sẽ bị kết tội cướp ngân hàng, nhưng do có khai báo đồng bọn nên được hưởng mức án nhẹ hơn so với PH và HP (4 năm tù).
Lý luận:
- Lựa chọn “Phản bội” luôn hấp dẫn hơn “Giữ im lặng”: Đối với mỗi tên tù nhân, lựa chọn “Phản bội” luôn mang lại lợi ích cá nhân cao hơn, bất kể lựa chọn của người kia là gì.
- Cân bằng Nash: Vì “Phản bội” là lựa chọn tối ưu cho mỗi tên tù nhân, cả hai sẽ đều chọn “Phản bội”. Đây là cân bằng Nash của trò chơi.
Kết quả:
Dù cả hai cùng phản bội dẫn đến mức án thấp hơn so với cùng giữ im lặng, nhưng điều này vẫn không phải là kết quả tốt nhất cho cả hai. Nếu cả hai cùng giữ im lặng, họ chỉ chịu án 2 năm tù.
Một số thành phần chính trong lý thuyết trò chơi
Người chơi
- Là các cá nhân hoặc nhóm tham gia vào trò chơi.
- Mỗi người chơi có mục tiêu và sở thích riêng.
- Ví dụ: Trong “Thế lưỡng nan của tù nhân”, hai tên tù nhân là hai người chơi.
Chiến lược
- Là tập hợp các hành động mà mỗi người chơi có thể lựa chọn.
- Mỗi chiến lược có thể dẫn đến kết quả khác nhau.
- Ví dụ: Trong “Thế lưỡng nan của tù nhân”, mỗi tên tù nhân có hai chiến lược: “Giữ im lặng” và “Phản bội”.
Thông tin
- Mức độ thông tin mà mỗi người chơi có về các chiến lược của người chơi khác.
- Có hai loại thông tin chính: “Hoàn chỉnh” và “Thiếu”.
- Ví dụ: Trong “Thế lưỡng nan của tù nhân”, mỗi tên tù nhân không biết lựa chọn của người kia (thông tin thiếu).
Kết quả
- Là kết quả của trò chơi, được xác định bởi chiến lược của tất cả người chơi.
- Mỗi kết quả có thể mang lại lợi ích hoặc tổn hại cho từng người chơi.
- Ví dụ: Trong “Thế lưỡng nan của tù nhân”, kết quả phụ thuộc vào lựa chọn của cả hai tên tù nhân.
Cân bằng Nash
- Là tập hợp các chiến lược, trong đó mỗi người chơi không thể cải thiện lợi ích của mình bằng cách thay đổi chiến lược của mình, giả sử các chiến lược của người chơi khác không thay đổi.
- Cân bằng Nash có thể là duy nhất hoặc có nhiều.
Ví dụ: Trong “Thế lưỡng nan của tù nhân”, “cả hai cùng phản bội” là một cân bằng Nash.
Loại trò chơi
- Phân loại theo số lượng người chơi, thông tin, chiến lược, và kết quả.
Ví dụ: “Thế lưỡng nan của tù nhân” là một trò chơi hai người chơi, thông tin thiếu, chiến lược thuần túy, và tổng bằng không.
Cân bằng Nash là gì?
Cân bằng Nash (Nash equilibrium) là tình huống mà không người chơi nào có thể cải thiện lợi ích của mình bằng cách thay đổi chiến lược. Tình huống này giống như đạt được trạng thái cân bằng lý tưởng. Khi ấy, mỗi người chơi đều hài lòng với cách hành động đã chọn vì hành động đó mang lại phần thưởng tốt nhất cho họ. Miễn là tất cả những người chơi khác đều tuân theo kế hoạch của mình thì không ai có lý do để thay đổi cách chơi.
Cân bằng Nash là một trạng thái ổn định. Trạng thái này giúp chiến lược của bạn không ảnh hưởng đến lựa chọn của người chơi khác. Vì vậy, việc bạn tiếp tục sử dụng chiến lược hiện tại là hợp lý.
Phân loại lý thuyết trò chơi
Theo thông tin từ trang Britannica trong bài “Game Theory”, lý thuyết trò chơi được phân loại như sau:
Trò chơi có thể được phân loại dựa trên một số đặc điểm quan trọng, trong đó dễ thấy nhất là số lượng người chơi. Do đó, một trò chơi có thể được phân thành trò chơi một người, hai người hoặc n người (với n lớn hơn hai), với các trò chơi trong mỗi loại có những đặc điểm riêng biệt. Ngoài ra, người chơi không nhất thiết phải là một cá nhân. Người chơi có thể là một quốc gia, một tập đoàn hoặc một đội gồm nhiều người có cùng lợi ích.
Lý thuyết trò chơi sẽ được phân loại theo 3 yếu tố sau:
- Theo thông tin.
- Theo mục tiêu.
- Theo tính hữu hạn.
Phân loại theo thông tin
- Trò chơi thông tin hoàn hảo: Trong các trò chơi thông tin hoàn hảo, chẳng hạn như cờ vua, mỗi người chơi đều biết mọi thứ về trò chơi mọi lúc.
- Trò chơi thông tin không hoàn hảo: Mặt khác, poker là một ví dụ về trò chơi thông tin không hoàn hảo vì người chơi không biết tất cả các lá bài của đối thủ.
Phân loại theo mục tiêu
- Trò chơi tổng bằng không: Là trò chơi đối đầu hoàn toàn, còn được gọi là trò chơi cạnh tranh thuần túy. Poker, chẳng hạn, là một trò chơi tổng bằng không vì tổng tài sản của người chơi luôn không đổi, mặc dù cách phân bổ có thể thay đổi trong quá trình chơi. Người chơi trong các trò chơi tổng bằng không có lợi ích hoàn toàn đối lập, trong khi trong các trò chơi tổng biến đổi, tất cả người chơi đều có thể thắng hoặc thua. Ví dụ, trong tranh chấp lao động – quản lý, hai bên chắc chắn có một số lợi ích mâu thuẫn, nhưng cả hai sẽ được hưởng lợi nếu tránh được đình công.
Trò chơi tổng biến đổi có thể được phân biệt thêm thành hợp tác hoặc không hợp tác.
- Trò chơi hợp tác: Người chơi có thể giao tiếp và quan trọng nhất là đưa ra các thỏa thuận ràng buộc; trong các trò chơi không hợp tác, người chơi có thể giao tiếp, nhưng họ không thể đưa ra các thỏa thuận ràng buộc, chẳng hạn như hợp đồng có thể thực thi. Một nhân viên bán ô tô và khách hàng tiềm năng sẽ tham gia vào một trò chơi hợp tác nếu họ đồng ý về giá cả và ký hợp đồng. Tuy nhiên, quá trình mặc cả để đạt được mục tiêu này sẽ là không hợp tác. Tương tự, khi mọi người tham gia đấu giá độc lập, họ đang chơi một trò chơi không hợp tác, ngay cả khi người trả giá cao nhất đồng ý hoàn tất việc mua hàng.
Phân loại theo tính hữu hạn
Cuối cùng, một trò chơi được gọi là hữu hạn khi mỗi người chơi có một số lựa chọn hữu hạn, số lượng người chơi là hữu hạn và trò chơi không thể diễn ra vô thời hạn. Cờ vua, cờ caro, poker và hầu hết các trò chơi trong nhà đều là hữu hạn. Trò chơi vô hạn phức tạp hơn và sẽ chỉ được đề cập sơ lược trong bài viết này.
Các dạng mô tả trò chơi
Một trò chơi có thể được mô tả theo một trong ba cách:
- Dạng mở rộng.
- Dạng chuẩn.
- Dạng hàm đặc trưng.
Đôi khi các dạng này được kết hợp, như được mô tả trong phần Lý thuyết về các nước đi. Hầu hết các trò chơi trong nhà, diễn ra từng bước, từng bước đi một. Chúng có thể được mô hình hóa thành các trò chơi dạng mở rộng.
Dạng mở rộng
Trò chơi dạng mở rộng có thể được mô tả bằng một “cây trò chơi”, trong đó mỗi lượt chơi là một đỉnh của cây, với mỗi nhánh cho biết các lựa chọn liên tiếp của người chơi.
Dạng chuẩn
Dạng chuẩn (chiến lược) chủ yếu được sử dụng để mô tả các trò chơi hai người. Trong dạng này, một trò chơi được biểu diễn bằng ma trận lợi ích, trong đó mỗi hàng mô tả chiến lược của một người chơi và mỗi cột mô tả chiến lược của người chơi khác. Mục nhập ma trận tại giao điểm của mỗi hàng và cột cho kết quả của việc mỗi người chơi chọn chiến lược tương ứng. Lợi ích cho mỗi người chơi liên quan đến kết quả này là cơ sở để xác định xem các chiến lược có “cân bằng” hay ổn định không.
Dạng hàm đặc trưng
Dạng hàm đặc trưng thường được sử dụng để phân tích các trò chơi có nhiều hơn hai người chơi. Với dạng này, chúng sẽ biết giá trị tối thiểu mà mỗi liên minh người chơi – bao gồm cả liên minh một người chơi – có thể đảm bảo cho chính mình khi chơi chống lại một liên minh gồm tất cả những người chơi khác.
Tại sao lý thuyết trò chơi lại quan trọng?
Lý thuyết trò chơi đóng vai trò quan trọng trong nhiều lĩnh vực vì 3 lý do dưới đây.
1. Hiểu hành vi của con người trong các tình huống chiến lược
Trong thế giới ngày càng cạnh tranh, việc hiểu được bản chất của đàm phán và mặc cả là điều cần thiết. Lý thuyết trò chơi giúp bạn dự đoán hành vi của mọi người khi họ ở trong một tình huống cạnh tranh. Bạn có thể sử dụng thông tin này để hiểu rõ hơn về những người xung quanh và lựa chọn chiến lược tốt nhất để đạt được mục tiêu hoặc giải quyết vấn đề.
2. Hiểu thị trường và hoạt động kinh doanh
Lý thuyết trò chơi ngày càng có giá trị trong lĩnh vực marketing, giúp các nhà tiếp thị dự đoán hành vi ra quyết định của người tiêu dùng. Giải pháp này cũng rất hữu ích cho các doanh nghiệp mô hình hóa hoạt động của thị trường. Lý thuyết trò chơi có thể giúp các nhà quản lý lựa chọn chiến lược tốt nhất để thu hút, giữ chân, thỏa mãn và xây dựng mối quan hệ khách hàng. Thông tin này cũng có thể giúp lập kế hoạch tuyển dụng nhân sự, đào tạo và phát triển chiến lược.
3. Đánh giá hiệu quả ra quyết định trong cộng đồng
Lý thuyết trò chơi có thể giúp đánh giá mức độ hiệu quả của việc ra quyết định trong cộng đồng khi không có sự hợp tác giữa những người chơi. Bạn có thể sử dụng lý thuyết trò chơi để dự đoán hành vi của mọi người trong một số tình huống nhất định, cho phép bạn đưa ra quyết định sáng suốt hơn về cách hành động tốt nhất. Thông tin này cũng là chìa khoá để bạn lập kế hoạch chính sách ảnh hưởng đến toàn bộ cộng đồng.

4 điểm hạn chế của lý thuyết trò chơi
Ngoài những lợi ích thiết thực, lý thuyết trò chơi cũng có các điểm hạn chế nhất định. Dưới đây là 4 điểm hạn chế của lý thuyết trò chơi.
Dựa trên giả định
Lý thuyết trò chơi sử dụng các mô hình toán học và giả định. Mặc dù những giả định này có thể gần với thực tế, nhưng chúng có thể không phản ánh chính xác thế giới thực.
Ví dụ, lý thuyết trò chơi thường cho rằng mọi người đều lý trí, ích kỷ và cạnh tranh – nhưng trong thực tế, mọi người thường không hợp lý hoặc không quan tâm đến việc cạnh tranh với người khác.
Phạm vi hạn chế
Bạn không thể giải quyết mọi trò chơi bằng các mô hình toán học đơn giản như những mô hình mà lý thuyết trò chơi sử dụng. Ví dụ, việc tạo mô hình để giải quyết một trò chơi có thể trở nên phức tạp nếu có quá nhiều người chơi và nước đi tiềm năng.
Mỗi hành động có thể dẫn đến quá nhiều kết quả hoặc người chơi có thể hưởng lợi từ nhiều chiến lược. Ngoài ra, người chơi không phải lúc nào cũng hành động theo cách có thể dự đoán được hoặc hợp lý. Do đó, lý thuyết trò chơi không phù hợp với tất cả các tình huống.
Dễ bị hiểu sai
Mọi người thường hiểu sai về lý thuyết trò chơi và áp dụng sai vào thế giới thực. Ví dụ, họ có thể cho rằng lý thuyết trò chơi chỉ dành cho các tình huống cạnh tranh. Do đó, họ chỉ có thể tập trung vào khía cạnh cạnh tranh thay vì các yếu tố khác, chẳng hạn như lòng trung thành hoặc sự tin tưởng. Hiểu sai về lý thuyết trò chơi khiến mọi người có nguy cơ đưa ra những quyết định không chính xác.
Sự bất ổn
Lý thuyết trò chơi không bao gồm yếu tố bất ổn, điều quan trọng đối với một số tình huống nhất định. Ví dụ, việc sử dụng lý thuyết trò chơi trong quá trình đàm phán hoặc khi đưa ra các quyết định ảnh hưởng đáng kể đến hoạt động kinh doanh sẽ rất khó khăn. Nếu bạn không chắc chắn về nước đi tiếp theo của đối thủ cạnh tranh, việc lựa chọn chiến lược tốt nhất cho mình có thể gặp khó khăn.
Ứng dụng của lý thuyết trò chơi trong các lĩnh vực
Kinh tế
- Phân tích thị trường: Lý thuyết trò chơi trong kinh tế học được sử dụng để mô hình hóa hành vi của các doanh nghiệp trong thị trường cạnh tranh, giúp dự đoán giá cả, sản lượng và chiến lược của doanh nghiệp.
- Đấu giá: Lý thuyết trò chơi được sử dụng để phân tích chiến lược đấu giá của người mua và người bán, giúp dự đoán giá bán và chiến thắng trong các cuộc đấu giá.
- Đàm phán hợp đồng: Lý thuyết trò chơi được sử dụng để phân tích chiến lược đàm phán của các bên liên quan, giúp đạt được thỏa thuận hợp lý và hiệu quả.
Khoa học chính trị
- Bầu cử: Lý thuyết trò chơi được sử dụng để mô hình hóa hành vi của các cử tri và ứng cử viên trong các cuộc bầu cử, giúp dự đoán kết quả bầu cử và chiến lược vận động tranh cử.
- Quan hệ quốc tế: Lý thuyết trò chơi được sử dụng để phân tích chiến lược của các quốc gia trong các vấn đề quốc tế, như chiến tranh, hòa bình và thương mại.
- Hợp tác quốc tế: Lý thuyết trò chơi được sử dụng để phân tích các vấn đề hợp tác quốc tế, như biến đổi khí hậu và chống khủng bố.
Kinh doanh
- Chiến lược kinh doanh: Lý thuyết trò chơi trong kinh doanh được sử dụng để phân tích chiến lược cạnh tranh của doanh nghiệp, giúp lựa chọn chiến lược tốt nhất để đạt được lợi thế cạnh tranh.
- Định giá sản phẩm: Lý thuyết trò chơi được sử dụng để phân tích chiến lược định giá của doanh nghiệp, giúp lựa chọn mức giá tối ưu để tối đa hóa lợi nhuận.
- Quản lý dự án: Lý thuyết trò chơi được sử dụng để phân tích chiến lược hợp tác giữa các bên liên quan trong dự án, giúp dự án thành công.

Sinh học
- Tiến hóa: Lý thuyết trò chơi được sử dụng để giải thích sự tiến hóa của các hành vi trong tự nhiên, như sự hợp tác và cạnh tranh giữa các loài.
- Sinh thái học: Lý thuyết trò chơi được sử dụng để phân tích các tương tác giữa các loài trong hệ sinh thái, giúp hiểu được sự cân bằng sinh thái và bảo tồn đa dạng sinh học.
Khoa học máy tính
- Trí tuệ nhân tạo: Lý thuyết trò chơi được sử dụng để phát triển các thuật toán trí tuệ nhân tạo, giúp máy tính có thể đưa ra quyết định tối ưu trong các tình huống chiến lược.
- Mạng lưới: Lý thuyết trò chơi được sử dụng để phân tích và thiết kế các mạng lưới, như mạng lưới máy tính và mạng lưới xã hội.
- An ninh mạng: Lý thuyết trò chơi được sử dụng để phân tích các cuộc tấn công mạng và phòng thủ mạng, giúp bảo vệ hệ thống mạng.
Kết luận
Nhìn chung, lý thuyết trò chơi là một công cụ mạnh mẽ giúp chúng ta hiểu được hành vi của con người trong các tình huống chiến lược. Công cụ này cung cấp cho chúng ta một khuôn khổ để phân tích các tương tác giữa các cá nhân hoặc tổ chức, dự đoán kết quả và đưa ra quyết định tốt hơn.
Hy vọng bài viết trên sẽ là nguồn tham khảo hữu ích khi bạn muốn tìm hiểu về lý thuyết trò chơi. Đừng quên theo dõi TinoHost để đón đọc những bài viết hay và hữu ích khác bạn nhé!
TÀI LIỆU THAM KHẢO
- Britannica. (2024, Feb 16). Game Theory. Britannica.com. https://www.britannica.com/science/game-theory
- Rutan Bhattacharyya. (2024, January 29). Game Theory. Wallstreetmojo.com. https://www.wallstreetmojo.com/game-theory-2/#types
- Indeed Editorial Team. (2022, December 19). What Is Game Theory? (Importance and Applications). Ca.indeed.com. https://ca.indeed.com/career-advice/career-development/game-theory
Những câu hỏi thường gặp
Lý thuyết trò chơi được sử dụng để làm gì?
Lý thuyết trò chơi được sử dụng để phân tích các tương tác giữa các cá nhân hoặc tổ chức, dự đoán kết quả và đưa ra quyết định tốt hơn trong nhiều lĩnh vực khác nhau.
Ma trận lợi nhuận là gì?
Ma trận lợi nhuận là một công cụ được sử dụng để mô tả lợi ích của mỗi người chơi trong một trò chơi, dựa trên các chiến lược mà họ lựa chọn.
Phân tích vấn đề kinh doanh bằng lý thuyết trò chơi được không?
Lý thuyết trò chơi có thể được sử dụng để phân tích các vấn đề kinh doanh, chẳng hạn như định giá và hợp tác. Ví dụ, Lý thuyết trò chơi có thể được sử dụng để mô hình hóa hành vi của các doanh nghiệp trong các cuộc đàm phán hợp đồng.
Trò chơi lặp lại là gì?
Trò chơi lặp lại là trò chơi được chơi nhiều lần với cùng một nhóm người chơi.



![Cách tạo workflow trên n8n cơ bản cho người mới bắt đầu [Hướng dẫn chi tiết]](https://wiki.tino.org/wp-content/uploads/2025/04/cach-tao-workflow-co-ban-tren-n8n-cover-150x150.png)





![Cách tạo workflow trên n8n cơ bản cho người mới bắt đầu [Hướng dẫn chi tiết]](https://wiki.tino.org/wp-content/uploads/2025/04/cach-tao-workflow-co-ban-tren-n8n-cover-260x176.png)







